Introduction Notes Theory HOWTO Examples Engineering Error Questions Matlab Maple

Example 1

Perform three approximations using Euler's method for the IVP

y⁽²⁾(t) = 4 − sin(t) + y(t) − 2 y⁽¹⁾(t)
y(0) = 1
y⁽¹⁾(0) = 2

with a step size of h = 0.1.

Using the rewritten derivative

we may calculate:

y₁ = y₀ + h f(0, y₀) = (1.2, 2.1)^T
y₂ = y₁ + h f(h, y₁) = (1.41, 2.1900166583)^T
y₃ = y₂ + h f(2h, y₂) = (1.62900166583, 2.2731463936)^T

Consequently, the approximation of the solution comprises the points

(0, 1), (0.1, 1.2), (0.2, 1.41), (0.3, 1.62900166583)

and the derivatives at these points are 2, 2.1, 2.1900166583, and 2.2731463936, respectively.

Example 2

Perform two approximations using Heun's method for the IVP

y⁽³⁾(t) = y(t) − t y⁽¹⁾(t) + 4 y⁽²⁾(t)
y(2) = 1
y⁽¹⁾(2) = 2
y⁽²⁾(2) = 3

with a step size of 0.1

In the theory section, we saw that this IVP can be converted into the system

and therefore, we may calculate:

K₀ = f( 0, y₀ ) = (2, 3, 13)^T
K₁ = f( h, y₀ + hK₀ ) = (2.3, 4.3, 18.17)^T

Therefore,

y₁ = y₀ + h (K₀ + K₀)/2 = (1.215, 2.365, 4.5585)^T

To approximate the next point, we repeat the process:

K₀ = f( h, y₁ ) = (2.365, 4.5585, 19.2125)^T
K₁ = f( 2h, y₁ + hK₀ ) = (2.82085, 6.47975, 26.80633)^T

Therefore,

y₂ = y₁ + h (K₀ + K₀)/2 = (1.4742925, 2.9169125, 6.8594415)^T

Consequently, the approximations to the solution are (0, 1), (0.1, 1.215), and (0.2, 1.4742925).

The derivatives at these three points are 2, 2.365, and 2.9169125, respectively, and the Nd derivatives at these points are 3, 4.5585, and 6.8594415, respectively.

Example 3

As an example of a stiff differential equation, you saw the Van der Pol 2nd-order ordinary differential equation:

y⁽²⁾(t) − μ(1 − y(t)²) y⁽¹⁾(t) + y(t) = 0

We can rewrite this in the desired form:

y⁽²⁾(t) = μ(1 − y(t)²) y⁽¹⁾(t) − y(t)

Let μ = 0.3 and let the initial conditions be y(0) = 0.7 and y⁽¹⁾(0) = 1.2 and therefore, we may convert this to the system:

and

with the initial conditions

For simplicity, we will explicitly solve this system using multiple steps of Euler's method. We deliberately choose a very small value of h = 0.1 to avoid the stiff properties of this ODE and we define t_i = ih. Thus, for i = 1, 2, ..., 1000, we will solve:

y_i = y_{i − 1} + h f( t_{i − 1}, y_{i − 1})

Therefore, for the first step, we have:

The next three iterations are

The term of primary interest is the first of each of the points. If we plot the points (t_i, y_{i, 1}), we get the oscillating curve in Figure 1.

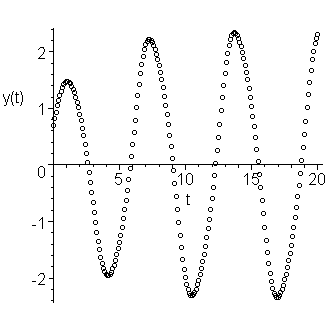
Figure 1. An approximation of the solution to our IVP.

Rather than plotting the points, we can connect the points with a line, as is shown in Figure 2.

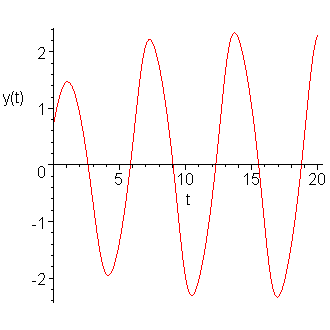
Figure 2. Plotting the approximation as a function.

If we plot (t_i, y_{i, 2}), we have an approximation to the derivative:

Figure 3. Plotting the approximation to the derivative of the solution to the IVP.

There appears to be a strong relationship between y(t) and y⁽¹⁾(t): this can be seen by plotting the solutions y_i, as is shown in Figure 4.

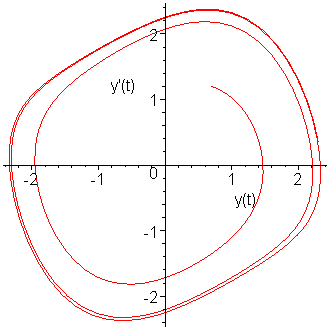
Figure 4. Plotting the vectors y_i.

These appear to be approaching a cyclic limit. If we plot the points y₁₉₃₅ through y₂₀₀₀, we note that the points form almost a perfect closed loop, as is shown in Figure 5.

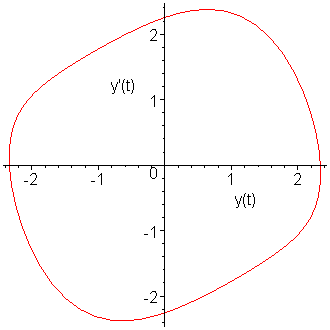
Figure 5. The limit cycle of our IVP.

Example 4

Consider a circuit with a single loop with an inductor of of 1 H, a resistor of 10 Ω and a capacitor of 0.25 F. If the system is initially at rest, and at time t = 0, a voltage force of x(t) = sin(t) for t ≥ 0 is applied. Solve for the current y(t) moving through the loop. This circuit is shown in Figure 6.

Figure 6. A linear circuit with an inductor, resistor, and a capacitor.

This system is described by the differential equation:

y⁽²⁾(t) + 10 y⁽¹⁾(t) + 4 y(t) = cos(t)
y(0) = 0
y⁽¹⁾(0) = 0

Again, we rewrite the ODE as

y⁽²⁾(t) = cos(t) − 10 y⁽¹⁾(t) − 4 y(t)

and define

with the initial conditions

The transfer function of this system is H(z) = z/(z² + 10z + 4), and therefore, the solution will approach y(t) = &re;(H(j) e^jt) = 10/109 cos(t). We will see if the numerical result is equivalent.

Seeing that cos(t) has a period of 2π, it would be appropriate to, once again, use h = 0.1. Thus, with

we find

Iterating many times, we get the approximation of the solution shown in Figure 7.

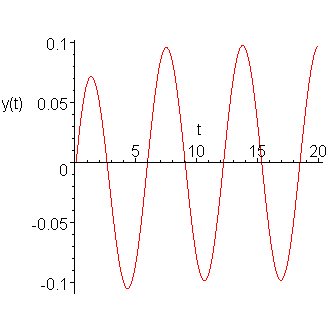
Figure 7. The solution to the forced circuit.

If we plot the approximations of the solution versus the derivative, we get the image in Figure 8.

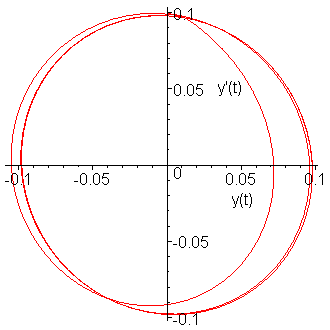
Figure 8. The solution versus the derivative.

From your circuits courses, you should expect such behaviour.

The maximum current should be 10/109 A, however, if we find the maximum approximate value of the current is 0.0980737, which is slightly greater than the expected maximum current.

Topic 14.8: Higher-Order Initial-Value Problems (Examples)

Example 1

Example 2

Example 3

Example 4