Question 1
Given the IVP shown in Example 4, find the first three iterations when then initial current -1 A. Use the value h = 0.1.
Answer: y1 = (-1.0, 0.5)T, y2 = (-0.95, 0.499500)T, y3 = (-0.90005, 0.479500)T.
Question 2
Given the IVP shown in Example 2, find the first three iterations when the forcing function is v(t) = e-t for t ≥ 0. Replace the cos(t) with the derivative of the new forcing function and use h = 0.1 and assume the system is initially at rest.
Answer: y1 = (0, -0.01)T, y2 = (-0.01, -0.11052)T, y3 = (-0.021052, -0.10652)T.
Question 3
Consider the circuit in Figure 1.
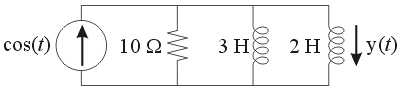
Figure 1. An RLL circuit.
From your circuits course, you can determine that the differential equation describing the current flowing across the second inductor is given by:
Rewrite this as a system of 1st-order differential equations.
Question 3
Given the 3rd-order IVP
y(0) = 3
y(1)(0) = 2
y(2)(0) = 1
Approximate y(1) by using one step of Euler's method and then again, by using 2 and then 4 steps of Euler's method.
Answer: (5, 3, 2)T; (4, 2.5, 1.5)T and (5.25, 3.25, 1.5)T; (3.5, 2.25, 1.25)T, (4.0625, 2.5625, 1.375)T, (4.703125, 2.90625, 1.40625)T, and (5.4296875, 3.2578125, 1.35546875)T.
Question 4
Given the 3rd-order IVP
y(0) = 3
y(1)(0) = 2
y(2)(0) = 1
Approximate y(1) by using one step of Euler's method and then again, by using 2 and then 4 steps of Euler's method.
Answer: (5, 3, 0)T; (4, 2.5, 0.5)T and (5.25, 2.75, 0.375)T; and (3.5 2.25 0.75)T, (4.0625 2.4375 0.578125)T, (4.671875 2.58203125 0.474609375)T, (5.3173828125 2.70068359375 0.42565917975)T.
Copyright ©2005 by Douglas Wilhelm Harder. All rights reserved.


