We have seen numerous techniques for working with an IVP which consists of a single 1st-order ODE and one initial condition. In this topic, we will look at how we can use the same techniques for solving a system of n 1st-order ODEs with n initial values.
Background
Useful background for this topic includes:
- 4. Linear Algebra
- 14.1 Euler's Method
References
- Bradie, Section 7.8, Systems of Equations and Higher-Order Equations, p.623.
- Mathews, Section 9.7, Systems of Differential Equations, p.518.
Theory
Consider the following system of two ODEs:
y(1)(t) = −4 x(t) − 6 y(t) − 2
where we have two initial conditions:
y(0) = 5
If we define the vector-valued function u(t) as
and then define
we may rewrite the system of ODEs as:
where f is the vector-valued function
Notice that this form is almost identical to the case with a single ODE:
y(t0) = y0
except that all of the functions u(t) and f(t, u) are now vector-valued instead of scalar-valued.
Now, whenever we did any operations in any of the methods, Euler, Huen, Runge-Kutta, or RKF45, the only operations were to:
- Evaluate f(t, y) at some point (t, y) or perhaps (t + h, y + hK),
- Add a scalar multiple of this onto the previous value yk.
These are vector as well as scalar operations, and therefore, we can do the same thing with these functions.
Example
Letting h = 0.1 and using Euler's method, then
Iterating a number of times, we get the sequence u0 through u6 of:
If we plot the first 21 points u0 through u20, we get the points shown in Figure 1.
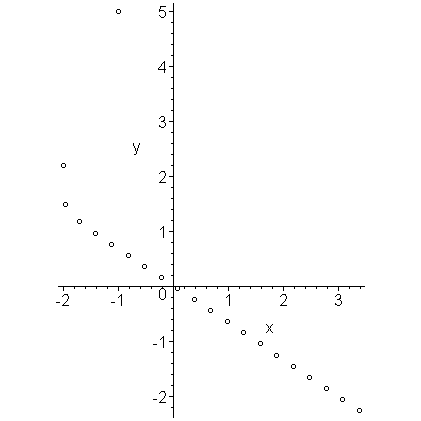
Figure 1. The first twenty approximations to the given IVP.
We can solve this IVP exactly to get that:
y(t) = 13/4 e−8 t − 2 t + 7/4
If we plot this curve for t between 0 and 2, we get the plot in Figure 2.

Figure 2. The first twenty approximations to the solution of the given IVP.
If x(t) and y(t) represent positions within a plane, then the solution u(t) = (x(t), y(t))T represents the movement of the particle in the plane as time passes. To emphasize this, Figure 3 is an animation showing the path followed by the particle.

Figure 3. An animation of the solution to the IVP.
For this, we used Euler's method, however, it would not be any different to use the 4th-order Runge-Kutta method (or even RKF45). If we use a step size of h = 0, the calculation of u1 would include:
Calculating the weighted average, we get:
Thus, the next point is
This first approximation is shown in Figure 4.
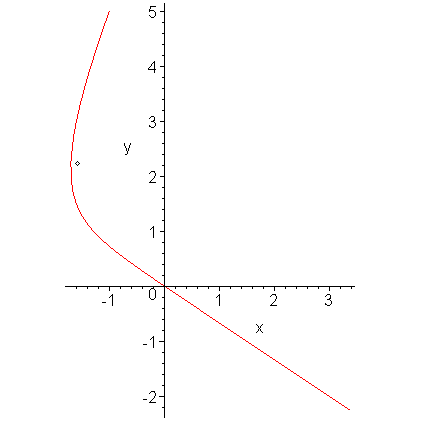
Figure 4. The first approximation using 4th-order Runge-Kutta.
If we plot the first 10 approximations, we get the points in Figure 5.
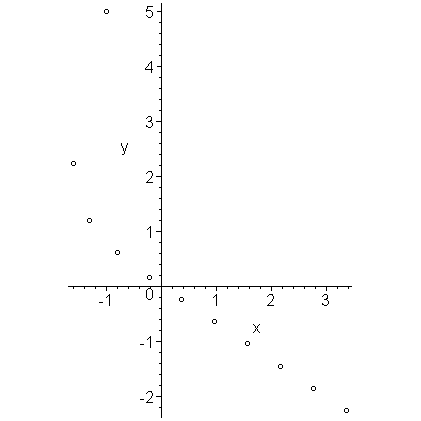
Figure 5. The first ten approximations using 4th-order Runge-Kutta.
Figure 6 compares the approximations with the actual solution. The approximations are in black while the actual values are in red. The initial significant difference between the approximations and the actual solutions and the closeness of subsequent approximations would suggest that this IVP is well suited for RKF45.
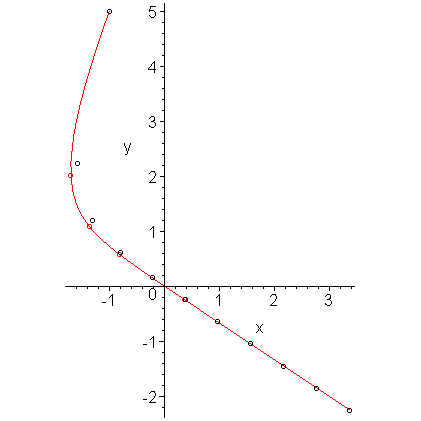
Figure 6. The approximations plotted with the actual solution.
HOWTO
Problem
Given the vector u(t) = (u1(t), ..., un(t))T, where, for each function uk(t), we have a first-order ODE deined by:
then we may define
where
Given this, together with the initial value u(t0) = u0 = (u0,1, ..., u0,n)T, we would like to approximate the solution to this IVP.
Assumptions
The function f(t, u) is continous.
Tools
We will use Euler, Heun, and 4th-order Runge Kutta, though the extension to RKF45 is straight-forward.
Process
Given a step size h, then tk = t0 + kh. We now examine how each method may be implemented.
Euler
Given uk, let:
Heun
Given uk, let:
K1 = f(tk + h, uk + hK0)
Then we define:
4th-order Runge Kutta
Given uk, let:
K1 = f(tk + ½h, uk + ½hK0)
K2 = f(tk + ½h, uk + ½hK1)
K3 = f(tk + h, uk + hK2)
Then we define:
Examples
Example 1
Almost all students have seen the butterfly effect, shown here on Wikipedia.
This is the result of a system of three non-linear differential equations collectively known as the Lorenz equations:
where
These variables represent certain properties of the earth's atmosphere. If we start with an initial condition of the atmosphere, then the differential equation dictates how the properties change over time.
For demonstration purposes, we will use σ = 10, ρ = 28, and β = 2.7
If we start with the initial point u0 = (1, 1, 1)T and use the function
together with a step size of h = 0.01, then applying Euler's method, we can calculate u1:
If we repeat this 1000 times, we can plot the result, as shown in Figure 1.
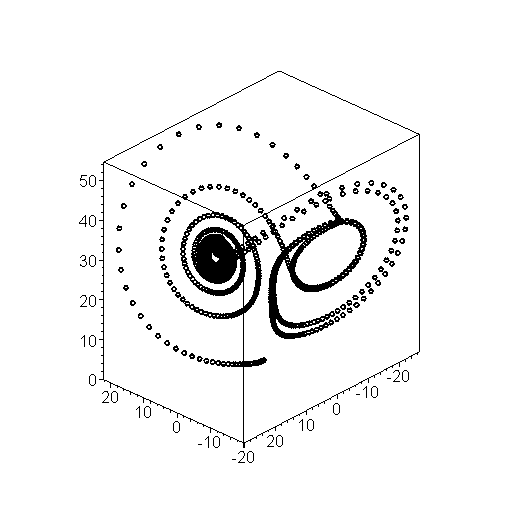
Figure 1. The first 1000 approximations for the solution to the Lorenz equations (click to enlarge).
This indicates that each of the three values varies over time, however, the first two variables do not move outside the range [-20, 20] while the third variable appears to be bounded by [0, 50].
It is more common to interpolate the points, as is shown in Figure 2.

Figure 2. The first 10000 approximations for the solution to the Lorenz equations (click to enlarge).
That the solution to this differential equation follows such a peculiar path is part of the study of chaos theory.
Engineering
To be completed.
Error
The error analysis for a system of IVPs is similar to that of an IVP with just one ODE.
Questions
Question 1
Consider the system of IVPs defined by
y(1)(t) = -2.6 x(t) − 0.3 y(t)
together with
Find the first five iterations using h = 0.1.
You can check your answer with
>> M = [-0.6 1.8; -2.6 -0.3];
>> x = zeros( 2, 1000 );
>> x(:, 1) = [1 1]';
>> for i=2:1000
x(:, i) = x(:, i - 1) + 0.1 * M*x(:, i - 1);
end;
>> plot( x(1, :), x(2, :) )
however, the first two iterations are u1 = (1.12, 0.71)T and u2 = (1.1806, 0.3975)T.
Matlab
If the IVP is linear, that is, the function f may be written as
for a matrix M and vector b, then we can very easily use Matlab to solve such systems.
For example, given the IVP
y(1)(t) = -2.6 x(t) − 0.7 y(t) + 0.8
x(0) = 1
y(0) = 1
then we may assign M and b:
>> M = [-0.5 1.9; -2.6 0.7]; >> b = [0.4 0.8]';
We will store the iterations in the 2 × N matrix and assign the initial values to be the first column:
>> N = 10000; >> x = zeros( 2, N ); >> x(:, 1) = [1 1]';
Next, we iterate Euler's method by assigning to the next column:
>> h = 0.01;
>> for i=2:N
x(:, i) = x(:, i - 1) + h*(M*x(:, i - 1) + b);
end;
To plot this data, we pass plot the first row (the x values) and the second row (the y values):
>> plot( x(1, :), x(2, :) )
The result of the first 10000 iterations is shown in Figure 1.
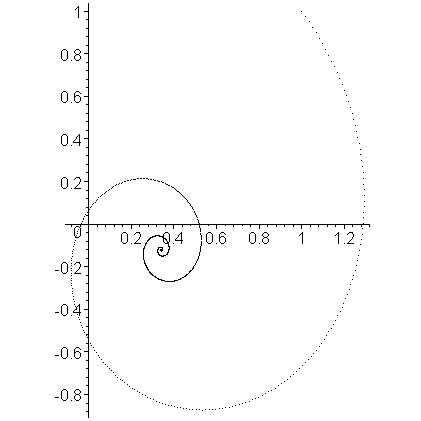
Figure 1. The first 10000 approximations of the solution to the system of IVPs (click to enlarge).
You may note that the solution appears to converge to a point. That point is the value of u such that Mu + b = 0, or Mu = −b. Thus, to find this point, we solve:
>> M \ (-b) ans = 0.340264650283554 -0.120982986767486
Heun's Method
To implement Heun's method, we need only one change:
>> for i=2:N
K0 = M*x(:, i - 1) + b;
K1 = M*(x(:, i - 1) + h*K0) + b;
x(:, i) = x(:, i - 1) + h*(K0 + K1)/2;
end;
4th-order Runge Kutta Method
To implement the 4th-order Runge Kutta method, we need only one change:
>> for i=2:N
K0 = M*x(:, i - 1) + b;
K1 = M*(x(:, i - 1) + h/2*K0) + b;
K2 = M*(x(:, i - 1) + h/2*K1) + b;
K3 = M*(x(:, i - 1) + h*K2) + b;
x(:, i) = x(:, i - 1) + h*(K0 + 2*K1 + 2*K2 + K3)/6;
end;
Maple
Maple works with an IVP consisting of a systems of ODEs as easily as it does with a single ODE.
dsolve( {
D(x)(t) = -2*x(t) − y(t) + 2,
D(y)(t) = −x(t) − 2*y(t) − 1,
x(0) = 1,
y(0) = 1
} );
This results in the solution
dsolve( {
D(x)(t) = -0.5*x(t) + 1.9*y(t) + 0.4,
D(y)(t) = -2.6*x(t) - 0.7*y(t) + 0.8,
x(0) = 1,
y(0) = 1
} ):
evalf(%);
{ x(t) = 0.34026 + exp(-0.6 t) ( 0.98896 sin(2.2204 t) + 0.65973 cos(2.2204 t)),
y(t) = -0.12098 + exp(-0.6 t) (-0.82302 sin(2.2204*t) + 1.12098 cos(2.2204 t)) }
Plotting this solution for t = [0, 15], we get the result shown in Figure 1.
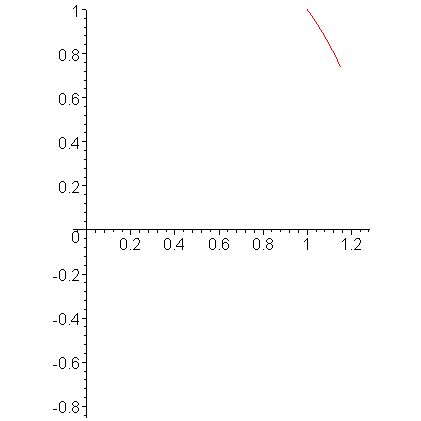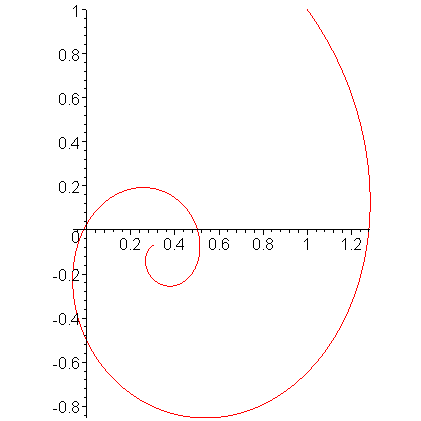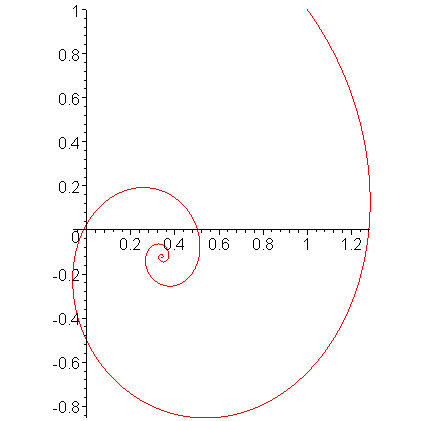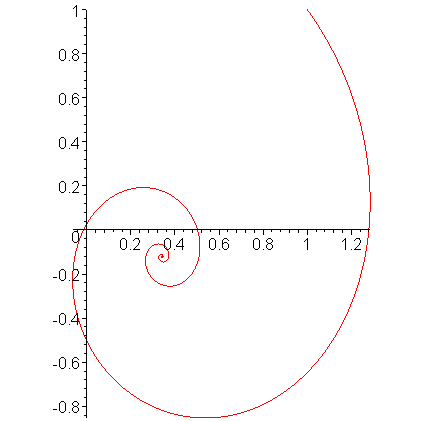
Figure 1. The solution to the initial value problem shown above.
Copyright ©2006 by Douglas Wilhelm Harder. All rights reserved.


