This is an implementation of Ian Munro and Hendra Suwanda's bi-parental heaps: a heap data structure where each node has two children and one or two parents and where each node must be both less than any children and greater than any parent.

Figure 1 shows a bi-parental heap with 17 objects.

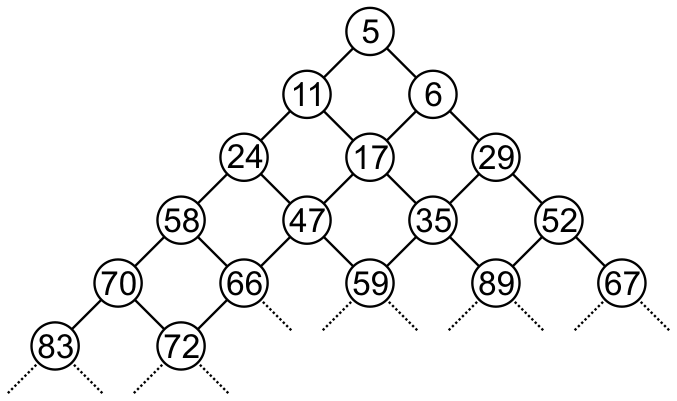
Figure 1. A bi-parental heap.

The strength and weakness of a bi-parental heap is that the height of the heap is approximately √2√n and the average depth of a node is approximately 2/3h and therefore all operations are O(√n) including arbitrary find and count functions while maintaining a run time Θ(1) access to the top element. In this spirit, this implementation, in addition, ensures that the unused memory is nevery greater than O(√n).

A bi-parental heap may be stored as an array (like a binary heap) but determining membership or finding the largest object are O(n) operations. Using an AVL tree will allow all operations to run in Θ(ln(n)) run time this is a node-based storage format requiring Θ(n) additional memory.

Insertions (pushes) occur at the next empty location, shown in Figure 2, and are percolated up.

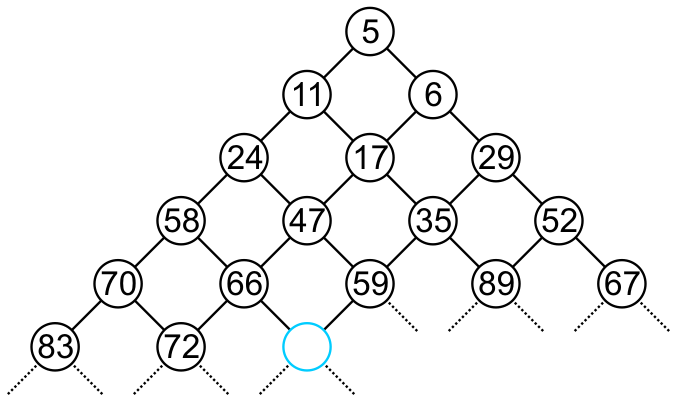
Figure 2. Insertion into a bi-parental heap.

Searching may be performed in O(√n) run time as is shown in Figure 3 which demonstrates the trace of a search for the value 44.

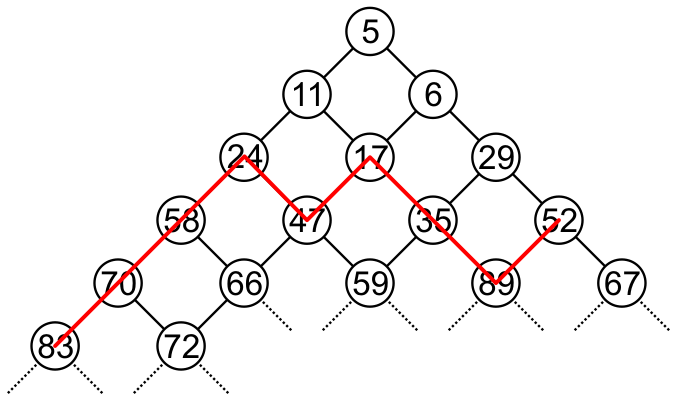
Figure 3. A search through a bi-parental heap for 44.

Bi-parental Heap
class Beap<Type>

Constructors

Beap<Type>( int h = 3 )

The constructor creates a bi-parental heap of initial capacity for a heap of height h. By default, this is 3 storing 10 objects.

Beap<Type>( Beap const &beap )

The constructor creates a bi-parental heap which is an exact copy of the argument.

Destructor

~Beap<Type>()

The destructor deallocates the memory used by the array.

Assignment

Beap<Type> &Beap<Type>::operator=( Beap<Type> const &rhs )

Assignment makes a deep copy of the right-hand side of the assignment.

Accessors

bool empty() const

The empty function returns true if the heap is empty and false otherwise. (Θ(1))

int size() const

The size function returns the number of objects stored within the bi-parental heap. (Θ(1))

int capacity() const

The capacity function returns the current capacity of the data structure storing the bi-parental heap. (Θ(1))

int height() const

The height function returns the height of the bi-parental heap. (Θ(1))

Type top() const

The top function returns the object at the top of (i.e., the next object to be popped from) of the bi-parental heap. If the heap is empty, Type() is returned. (Θ(1))

Type back() const

The back function returns the object at the back of (i.e., currently the last object to be popped from) of the bi-parental heap. If the heap is empty, Type() is returned. (Θ(√n))

bool find( Type const &obj ) const

Determines if the argument obj is in the bi-parental heap. (Θ(√n))

int count( Type const &obj ) const

Returns the the number of occurances of the argument obj in the bi-parental heap. (Θ(√n))

Mutators

void push( Type const &obj )

Insert the argument obj into the bi-parental heap allowing duplication of objects. If the heap is full, add one more level to the heap. This ensures that the unused memory is O(√n). (Θ(√n))

void pop()

Remove the top from the bi-parental heap. If this causes two rows of the heap to be empty, a new heap without the bottom row is allocated. This ensures that the unused memory is O(√n). (Θ(√n))

void erase( Type const &obj )

Remove all copies of the argument obj from the bi-parental heap. Not yet implemented. (Ω(√n))

void clear()

The clear function empties the bi-parental heap. (Θ(n))