Presented is an implementation of the modified sparse row (MSR) format (also called the new Yale sparse matrix representation); however, there is a focus on clarity rather than efficiency. In this implementation, an M×N matrix of double-precision floating-point numbers is given the type Matrix<M, N> while N-dimensional column and row vectors are given the types Vector<N, COLUMN> (or Vector<N>) and Vector<N, ROW>.

Figure 1 demonstrates how an 8×8 matrix is stored using the new Yale sparse-matrix representation:

• The diagonal entries are stored in an array diagonal of size min(M, N), and
• The off-diagonal entries are stored as follows:
• The non-zero off-diagonal entries are stored in an array off_diagonal by placing them in order by traversing each row from the first to the last,
• The corresponding columns of the entry stored in location off_diagonal[j] is stored in the location column_index[j], and
• The entry row_index[i] stores the entry first entry of row i and therefore all entries in row i are stored along the entries row_index[i], ..., row_index[i + 1] - 1.

The diagonal entries are stored in a separate array to allow the fastest possible access. Most sparse matrices of interest to engineers do not have zero entries on the diagonal (and are often positive definite). Hence, the diagonal is very likely to be dense.

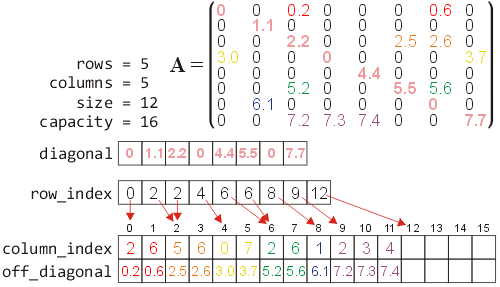
Figure 1. The sparse-matrix representation of an 8×8 matrix.

You will note that rows 1 and 4 have no off-diagonal entries and are therefore row_index[2] == row_index[1] and row_index[5] == row_index[4]. You will also note that the last entry of row_index always contains the number of off-diagonal entries, that is what is commonly referred to in the C++ STL as the size.

As one example of the simplifications used, a linear search is made of all the off-diagonal entries in a particular row. A binary search could be used, but this would obfuscate the code.

In the run-time analyzes, we will assume that the matrix is n×n, the number of non-zero off-diagonal entries are N, and the number of non-zero entries per row is approximately N/n.

Accessing entries in vectors and and matrices uses C-style indexing for i = 0, ..., M − 1; however, in some cases, it may be useful to access the last entry, row, or column without reference to the dimensions. Therefore, indices on the range i = -M, ..., -1 will access the entries M + i.

The following is a brief summary of the functions and operators provided with the package followed by a more detailed description of the individual functions. It is assumed the reader has a basic understanding of vector and matrix operaitons and therefore detailed descriptions of the functionality are not provided.

Contents

• Summary
• Vectors
• Vector Functionality
• Vector Functions
• Vector-Vector Operations
• Vector-Scalar Operations
• Vector Printing Operators and Functions
• Matrices
• Matrix Functionality
• Matrix Functions
• Matrix-Matrix Operations
• Matrix-Vector Operations
• Matrix-Scalar Operations
• Matrix Queries
• Solvers for Systems of Linear Equations
• Solvers for Systems of Linear Equations using Projection Methods
• Matrix Printing Operators and Functions

Summary

In this summary, A and B represent matrices, u and v represent vectors, α represents a real number, M and N are dimensions, i and j are indices (0 ≤ i < M and 0 ≤ j < N), and capacity is a nonnegative integer.

Functions

norm( v, 1 ), norm( v, 2 ), norm( v ), norm( A, 1 ), norm( A, 2 ), norm( A ) transpose( v ), transpose( A ), trace( A )

Operations

-A
v + α, α + v, A + α, α + B, u + v, u + B, A + v, A + B
v - α, α - v, A - α, α - A, u - v, u - B, A - v, A - B
v * α, α * v, A * α, α * B, u * v, u * B, A * v
v / α, α / v, A / α, u / v, u / B, A / v
matrix_vector_product( A, v, prod ), vector_matrix_product( u, A, prod )

v += α, A += α, u += v, A += v, A += B
v -= α, A -= α, u -= v, A -= v, A -= B
v *= α, A *= α, u *= v, A *= v
v /= α, A /= α, u /= v, A /= v

Solving

jacobi( A, v ), gauss_seidel( A, v )
backward_substitution( A, v, identity ), forward_substitution( A, v, identity ), diagonal_solve( A, v )

Contructors, Assignment, etc.

Vector<N, COLUMN> v( α ), Vector<N> v( α ), Vector<N, ROW> v( α ), Matrix<M, N> A( α, capacity )
Vector<N, COLUMN> v( u ), Vector<N> v( u ), Vector<N, ROW> v( u ), Matrix<M, N> A( B )
v(i), A(i, j), A.set( i, j, α ), A.set_symmetric( i, j, α ), A.clear( i, j ), A.clear()
u = v, A = B
Vector<N, COLUMN>::random() (or Vector<N>::random())
Vector<N, ROW>::random()
A.resize( capacity ), A.validate()

Printing

cout << A, cout << v
v.matlab( string str ), A.matlab( string str ), A.matlab_dense( string str ), A.details()

Vectors (Vector.h)

The Vector class stores a dense representation of an N-dimensional vector.

Vector Functionality (vector_mechanics.cpp)

Constructor:
Vector<N, COLUMN> v( double α ) (or Vector<N> v( double α ))
Vector<N, ROW> v( double α )

Create an N-dimensional column or row vector. All the entries are set to α (by default, 0.0).
O(N) time
O(N) memory

Indexing Operator:
v(int i)

Access the i^th entry of the vector v. It may be used either to access or change the value.

Copy Constructor:
Vector<N, COLUMN> v( u ) (or Vector<N> v( u ))
Vector<N, ROW> v( u )

The copy constructor makes deep copy of the vector—a new array is allocated and the entries are copied over.
O(N) time
O(N) memory

Assignment Operator:
u = v

The assignment operator makes deep copy of the vector—a new array is allocated and the entries are copied over.
vector v.
O(N) time
O(N) memory

Random Vector:
Vector<N, COLUMN>::random() (or Vector<N>::random())
Vector<N, ROW>::random()

Create vector with random entries on the interval (0, 1).
O(N) time
O(N) memory

Vector Functions (vector_functions.cpp)

norm( v, 1 ), norm( v, 2 ), norm( v )
v.norm( 1 ), v.norm( 2 ), v.norm()

The 1-, 2-, and ∞-vector norms of the vector v.
O(N) time
O(1) memory

transpose( v )

Generate a transpose of the vector v. The transpose of a row vector is a column vector and vice versa.
O(N) time
O(N) memory

Vector-Vector Operations (vector_vector_operations.cpp)

u + v, u += v
u - v, u -= v
u*v, u *= v
u/v, u /= v

If u and v are both either column vectors or row vectors, the vector-vector operations u + v, u − v, uv, and u/v are all interpreted element-wise yielding u_i + v_i, u_i − v_i, u_iv_i, and u_i/v_i, respectively. The operators +=, -=, *=, and /= are performed in place.
O(N) time
O(N) memory (O(1) if in place)

u*v

If u is a row vector and v is a column vector, then the product uv is the dot/inner product of the vectors.
O(N) time
O(1) memory

Vector-Scalar Operations (vector_scalar_operations.cpp)

v + α, v += α, α + v
v - α, v -= α, α - v

Add or subtract a scalar value α to each entry of a vector v. The special case α − v replaces each entry v_i with α − v_i. The operators += and -= are performed in place.
O(N) time
O(N) memory (O(1) if in place)

v*α, v *= α, α*v
v/α, v /= α, α/v

Multiply or divide a each entry of a vector v by a scalar value α, or divide a scalar value α by each entry of the vector. The special case α/v replaces each entry v_i with α/v_i. The operators *= and /= are performed in place.
O(N) time
O(N) memory (O(1) if in place)

Vector Printing Operators and Functions (vector_streaming.cpp)

cout << v

This operation prints the vector v as a row vector where column vectors are followed by a '.

v.matlab( string str )

The vector v is printed so that the output will recreate the vector in Matlab. For full precision, use cout.precision( 18 ); first. The string str is the variable name in Matlab to which the matrix will be assigned.

Matrices (Matrix.h)

The Matrix class stores a sparse representation of an M × N matrix.

Matrix Functionality (matrix_mechanics.cpp)

Constructor:
Matrix<M, N> A()
Matrix<M, N> A( double α, int capacity )

Create an M×N matrix. The diagonal entries are set to α (by default 0.0) and sufficient memory for capacity (by default 0) off-diagonal entries is allocated.
O(M) time
O(min(M, N)) or O(min(M, N) + capacity) memory

A(i, j)

Access the (i, j)^th entry of the matrix A. Assignment cannot be performed using this function. See set( i, j, α ).
O(1) time for a diagonal entry, O(n/N) time for an off-diagonal entry
O(1) memory

Note: using a binary search, the access time may be reduced to O(ln(n/N)).

A.set( i, j, double α )
A.set_symmetric( i, j, double α )

Set the (i, j)^th entry of the matrix to α. The symmetric version sets (j, i)^th to the same value. If the capacity of the storage for off-diagonal entries is full, the capacity is increased by 10.

Note: one could create a symmetric matrix representation which uses half the memory and some operations could per performed in half the time; however, the focus of this implementation is the basic representation. The viewer is welcome to contemplate the necessary modifications.

A.clear( i, j )

Set the (i, j)^th entry of the matrix to 0.0.

A.clear()

Set all entries in the matrix to 0.0. This is identical to multiplying a matrix by 0.0.

Copy Constructor:
Matrix<M, N> A( B )

The copy constructor makes a deep copy of the matrix.
O(M + n) time
O(M + c) memory

Assignment Operator:
A = B

Assignment makes a deep copy of the matrix.
O(M + n) time
O(M + c) memory

A.resize( int capacity )

Allocate memory for capacity (by default, 0) off-diagonal entries for the matrix; however, the capacity will not be reduced to below the current number of off-diagonal entries. To minimize the memory used by a matrix, call this function with no arguments.
O(M + n) time
O(M + c) memory

Matrix Functions (matrix_functions.cpp)

norm( A, 1 ), norm( A, 2 ), norm( A )
A.norm( 1 ), A.norm( 2 ), A.norm()

The 1-, 2-, and ∞-matrix norms of the matrix A.
1-norm: O(M + N + n) time and O(N) memory
2-norm: O(K(N + M + n)) time and O(N) memory
∞-norm: O(M + n) time and O(1) memory

trace( A )
A.trace()

The trace of the matrix A.
O(N) time
O(1) memory

transpose( A )

Generate a transpose of the matrix A. The transpose of a M × N matrix is an N × M matrix. The algorithm uses a heap-sort.
O(M + N + nln(n)) time
O(N + n) memory

-A

Negate each entry of the matrix A.
O(M + n) time
O(N + n) memory

A.validate()

This member function walks through the internal structure of the sparse matrix format to ensure that it is internally consistent:

• Sufficient memory is allocated (the capacity) for the number of off-diagonal entries,
• The row indices are monotonically (but not strictly) increasing with row_index[0] == 0,
• For each i = 1, ..., M, within the range j = row_index[i], ..., row_index[i + 1] - 1, the entries column_index[j] are strictly monotonically increasing and column_index[j] != i, that is, we are not storing a diagonal entry,
• All the off-diagonal entries are non-zero.

Matrix-Matrix Operations (matrix_matrix_operations.cpp)

A + B, A += B, A - B, A -= B

If A and B are M×N matrices, A + B and A - B are the element-wise operations a_ij + b_ij and a_ij − b_ij, respectively. The operations += and -= are performed in place.
O(M + n_A + n_B) time
O(M + n_A + n_B) memory (O(n_A + n_B) if in place)

Matrix-Vector Operations (matrix_vector_operations.cpp)

u*A, A*v
u *= A, A *= v

If u is an M-dimensional row vector, A is an M×N matrix, and v is an N-dimensional column vector then uA is an N-dimensional row vector and Av is an M-dimensional column vector. The operation *= are performed in place on the vector. Please note: A *= v modifies v and not A.br /> O(M + N + n) time
O(N) or O(M) memory (O(1) if in place)

A + v, A += v
A - v, A -= v

Assuming that the size of v is min(M, N), add or subtract the entries of the vector v from the diagonal of the matrix A. The operations += and -= are performed in place.
O(M + n) time (O(min(M, N) if in place)
O(M + n) memory (O(1) if in place)

matrix_vector_product( A, v, prod )
vector_matrix_product( u, A, prod )

Calculate the matrix-vector product Av or the vector-matrix product uA for the appropriately shaped and sized vectors and matrices. The third argument prod indicates whether the product should involve taking the product with all entries of the matrix (FULL, the default), just the diagonal entries assuming all other entries are zero (DIAGONAL), just the off-diagonal entries (OFF_DIAGONAL), just the upper or strict upper triangular entries (UPPER and STRICT_UPPER), and just the lower or strict lower triangular entries (LOWER and STRICT_LOWER).

The run time depends on operation performed.

Matrix-Scalar Operations (matrix_scalar_operations.cpp)

A + α, A += α, α + A
A - α, A -= α, α - A

Add or subtract a scalar value α to each entry of a diagonal of the matrix A. Thus, A - 1 is identical to subtracting off the identity matrix. The special case α − v replaces each entry a_{i, i} with α − a_{i, i} and all other non-zero entries are negated. The operators += and -= are performed in place.
O(min(M, N) time
O(M + n) memory (O(1) if in place)

A*α, A *= α, α*A
A/α, v /= α

Multiply or divide a each entry of a matrix A by a scalar value α. The special case α/v is not included as this would result in a dense matrix of NaN. The operators *= and /= are performed in place.
O(M + n) time
O(M + n) memory (O(1) if in place)

Matrix Queries (matrix_queries.cpp)

The member functions

• bool is_lower_triangular() const
• bool is_upper_triangular() const
• bool is_strict_lower_triangular() const
• bool is_strict_upper_triangular() const
• bool is_diagonal() const
• bool is_symmetric() const
• bool is_antisymmetric() const

return true or false based on whether the matrix satisfies the shape. All use O(1) memory. The first five run in O(min(M, N)) time, while the latter two run in O(M + n²/M) time.

Solvers for Systems of Linear Equations (matrix_solvers.cpp)

v = jacobi( A, b )

Solve the system Ax = b using the Jacobi method.
O(K(N + n)) time
O(N) memory

v = gauss_seidel( A, b )

Solve the system Ax = b using the Gauss-Seidel method.
O(K(N + n)) time
O(N) memory

v = backward_substitution( A, b, identity = false )

Solve the system Ax = b using backward substitution under the assumption that A is an upper-triangular matrix. Entries below the diagonal are ignored. If the third argument (by default false) is true, it is assumed that the diagonal are all equal to 1.
O(N + n) time
O(N) memory

v = forward_substitution( A, b, identity = false )

Solve the system Ax = b using forward substitution under the assumption that A is a lower-triangular matrix. Entries above the diagonal are ignored. If the third argument (by default false) is true, it is assumed that the diagonal are equal to 1.
O(N + n) time
O(N) memory

v = diagonal_solve( A, b )

Solve the system Ax = b under the assumption that A is a diagonal matrix. Entries off the diagonal are ignored. This solution is often a good initial approximation x₀ for an iterative solver. O(N) time
O(N) memory

Solvers for Systems of Linear Equations using Projection Methods (projection_methods.cpp)

The following three linear solvers use projective methods to solve the system of linear equations Ax = b:

• Gradient descent,
• Minimal residue, and
• Residual norm and steepest descent.

Matrix Printing Operators and Functions (matrix_streaming.cpp)

cout << A

This operation prints the matrix A as a grid format. The author must work on this function.

A.matlab( string str )

The matrix A is printed so that the output will recreate the vector in Matlab in a sparse format. The string str is the variable name in Matlab to which the matrix will be assigned.

A.matlab_dense( string str )

The matrix A is printed so that the output will recreate the vector in Matlab in a dense format. The string str is the variable name in Matlab to which the matrix will be assigned.

A.details()

The internal structure of the matrix A is printed so that the user can examine the allocation of memory and storage of the entries.

Comments

You may notice that no matrix transpose function or matrix-matrix multiplication operator is provided. There are few circumstances where a matrix product is necessary: the product (AB)v can more easily be calculated using A(Bv). It is also possible that the product of sparse matrices is itself dense. As for transpose, there may be certain points where it is necessary, but remember that (A^Tv) = (A^Tv)^TT = (v^TA)^T. Using a heap data structure, it is possible to create the transpose in O(n ln(n)) time with O(n) additional memory.

I have not included operators such as == or !=. The entries of the matrices are floating-point numbers. Consequently, it would be best to use norm( u - v ) and norm( A - B ) to determine if the vectors or matrices are sufficiently close.