Maze Generation

This algorithm makes use of the disjoint set data structure to create a maze of m × n rooms. This is done by creating a set of m × n disjoint rooms and then choosing walls, testing the adjacent rooms belong to the same union of rooms and if they are separate, remove the wall and take the union of the two unions of rooms. This program gives ASCII output and Figure 1 shows the output of a 10 × 10 maze.


+  +--+--+--+--+--+--+--+--+--+
|  |              |     |     |
+  +  +  +--+--+--+--+  +  +--+
|     |        |              |
+--+  +--+  +--+--+  +--+--+  +
|     |                 |     |
+--+  +--+--+  +--+  +--+--+--+
|           |     |  |     |  |
+--+--+--+--+--+  +  +--+  +  +
|     |  |  |  |  |           |
+--+  +  +  +  +--+  +  +--+--+
|              |     |        |
+  +  +  +  +--+--+  +  +  +--+
|  |  |  |           |  |     |
+  +--+--+--+  +--+--+--+--+  +
|     |           |     |     |
+  +--+--+--+  +--+--+  +  +  +
|     |        |  |  |  |  |  |
+--+--+  +--+--+  +  +  +--+  +
|                       |     |
+--+--+--+--+--+--+--+--+--+  +

Figure 1. A 10 × 10 maze.


The output file src/out contains the output of an 500 × 50 maze. The run time and memory requirements are Θ(mn).

The implementation of this maze generator uses two classes: a disjoint-set class and a permutation class. With this, the code for generating the maze is reduced to approximately 20 lines—including comments. The run time of this algorithm is O(mnα(mn)); which, for all intents and purposes, is Θ(mn). This says: it takes as much time to create a maze as it does to print it. The memory requirements are Θ(mn). The functionality of the permutation class is described here.

Permutations

To generate a maze, it is necessary to randomly choose walls. Therefore, it is necessary to avoid choosing the same wall twice; otherwise, the program could run for an arbitrary length of time. To select each wall only once, we need a permutation of the possible walls: we create an array with the n values we would like to permute. For example, Figure 2 holds the values 0 through 11.


Figure 2. An array of 12 integers.

Randomly choose a index between 0 and 11 and choose that entry to be the first number in the permutation: in this example, choose 9. Remove 9 and replace it with the last entry, 11 as is shown in Figure 3.


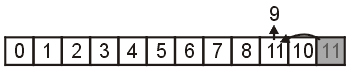
Figure 3. Selecting index 9 and replacing that entry with the last.

Again, choose a random index, but now between 0 and 10. In this example, the index is 4 and we replace that entry with the last entry 10. This is shown in Figure 4.


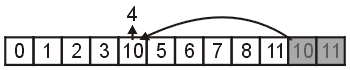
Figure 4. Selecting index 4 (from between 0 and 9) and replacing that entry with the last.

Choosing the random index 7 and replace it with the last entry (again 11), as is shown in Figure 5.


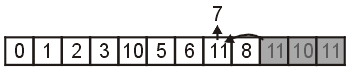
Figure 5. Select the random index 7 from (0 through 8) and replacing it with 8.

Figure 6 shows the next five steps: selecting index 5, 0, 2, 5, and 3. Up to this point, the permutation is 9, 4, 7, 5, 0, 2, 8, and 3.


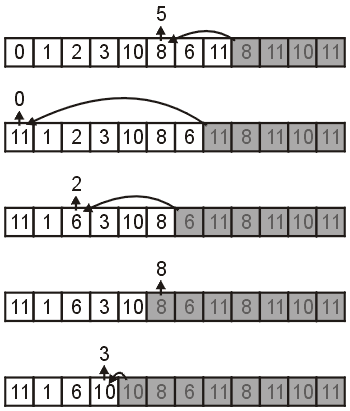
Figure 6. An array of 12 integers.

If the next four random numbers are 1, 2, 1, and 0, the random permutation of the numbers 0 through 11 are 1, 6, 10, and 11. Thus, the random permutation is:

9 4 7 5 0 2 8 3 1 6 10 11

Program 1 shows the printing of 100 numbers using the permutation class.

Program 1. Stepping through a permutation of 100 digits.

#include <iostream>
#include "Permutation.h"

int main() {
	Data_structures::Permutation n(100);

	for ( int i = 0; i < 100; ++i ) {
		std::cout << n.next() << " ";
	}

	return 0;
}

The output is:

83 43 37 22 17 65 16 12 57 59 32 96 82 31 99 56 24 38 44 10 11 1 3 81 26 5 92 7 19 98 71 21 80 91 29
95 49 72 78 45 9 18 53 20 48 89 50 40 70 90 13 75 51 15 2 58 6 30 88 42 25 46 60 79 84 74 67 85 61 39
54 0 97 28 93 64 27 76 94 14 62 63 47 69 73 66 52 55 23 41 36 68 4 87 86 35 33 8 77 34

A second execution of the function produces the permutation

95 91 80 53 59 51 9 26 41 70 52 16 21 56 46 94 87 92 24 23 40 37 45 25 83 71 93 0 77 8 67 79 1 48 54
76 10 29 17 27 28 4 81 82 31 58 72 15 68 32 84 78 36 90 65 63 38 49 64 86 19 55 12 11 69 44 33 43 34
18 57 89 3 85 7 88 47 35 73 98 66 2 61 14 97 30 39 62 13 74 75 22 60 99 6 20 50 96 5 42

If one was to instead simply continue to select random numbers from 0 to 99 and ignore duplication, it may take significantly longer to find a permutation. The most significant objection to the above algorithm for finding a permutation is that, by moving entries in the array, one will change the permutation. However, this does not affect the fact that the result is still random: in Figure 3 where 11 is moved to index 9, if the next index is randomly chosen between 0 and 10, whether 11 is in index 9 or 10 or anywhere else, it has equal probability of being selected as the next value in the permutation with all other remaining entries.