Inverse Square Root

A computation which occurs often in applications such as graphics is normalizing a vector. This requires both the calculation of a square root and a floating-point division—both of which are expensive operations. The following documents the implementation of an algorithm which computes a relatively fast inverse square root using simpler operations. This is documented more clearly on the Wikipedia page Fast inverse square root.

The Basic Algorithm

The source code for the basic algorithm is

float inv_sqrt( float x ) {
	int xi = *reinterpret_cast<int *>( &x );
	xi = INV_SQRT_N - (xi >> 1);
	return *reinterpret_cast<float *>( &xi );
}

where INV_SQRT_N is a magic number is chosen to minimize the error. Depending on which error one would like to minimize, be it the 1-, 2-, or ∞-norm, different magic numbers need to be used as is shown in Table 1.

Note: new-comers to C may wonder about the rather odd operation of taking the address of a float, casting it as a pointer to an integer, and then de-referencing this pointer: int *reinterpret_cast<int *>(&x). We cannot use static_cast<int>(x) because this will reinterpret the floating-point number by truncating the value to the greatest integer less than or equal to the value. The above formulation explicitly states: treat the bits of the floating-point number as if they were the bits of an integer.

Table 1. Optimal magic numbers for the three norms.

Magic Number
INV_SQRT_N		1-Norm of
Relative Error		2-Norm of
Relative Error		∞-Norm of
Relative Error
15972031790.015940.022240.05055
15972947870.017150.020930.04482
15974656470.023390.025280.03421

Figures 1 through 3 show the relative error of the approximations of 1/√x for values of x between 0.5 and 8. You will notice that the relative error repeats for each power of 4. Figures 1, 2, and 3 plot the error when using the constant which minimizes the 1-, 2-, and ∞-norms, respectively.


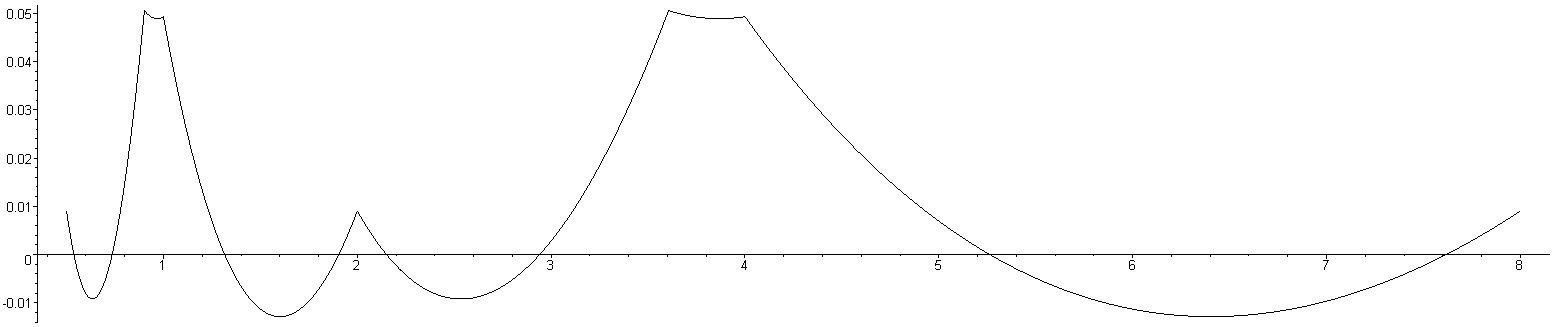
Figure 1. The relative error for the coefficient minimizing the 1-norm of the relative error.


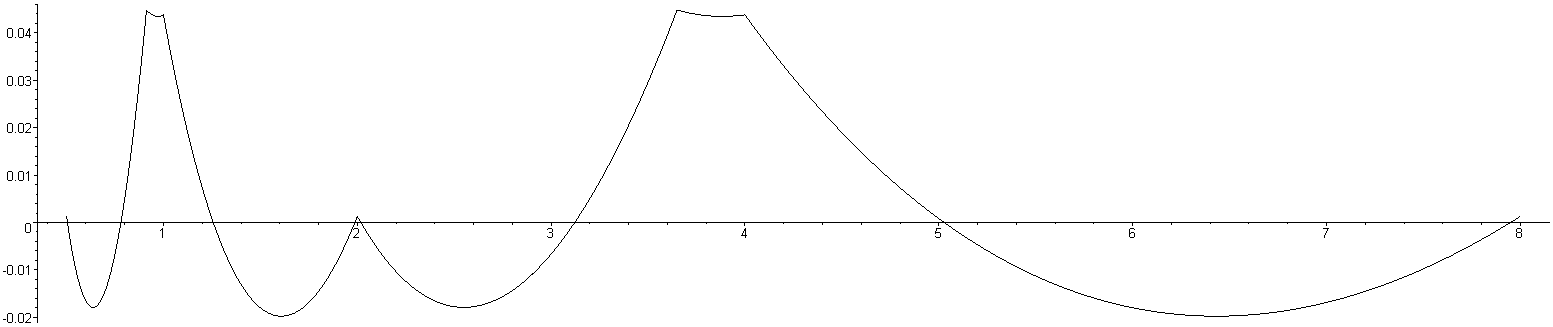
Figure 2. The relative error for the coefficient minimizing the 2-norm of the relative error.


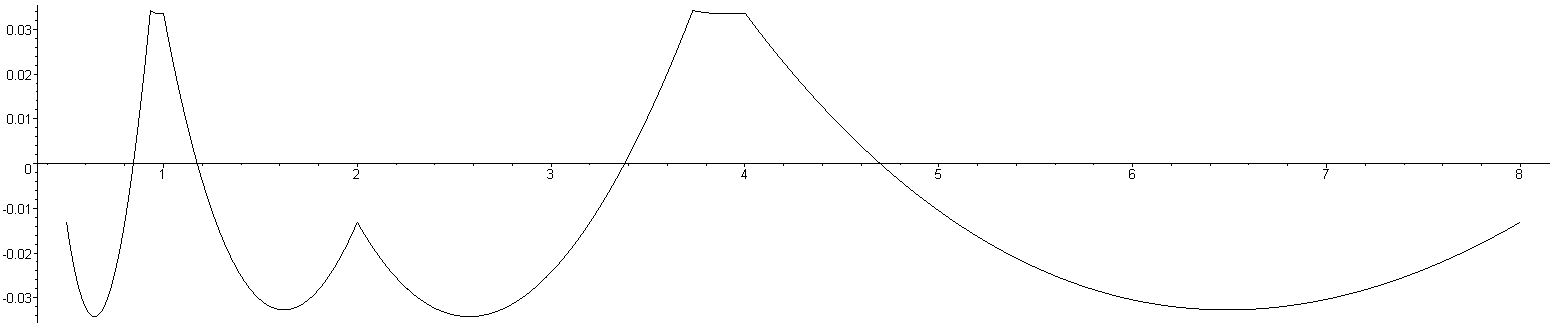
Figure 3. The relative error for the coefficient minimizing the ∞-norm of the relative error.

Applying Newton's Method

Applying one iteration of Newton's method reduces the error significantly.

float inv_sqrt_newton( float x ) {
	float const half_x0 = 0.5f*x;
	int xi = *reinterpret_cast<int *>( &x );
	xi = INV_SQRT_NEWTON_N - (xi >> 1);
	x = *reinterpret_cast<float *>( &xi );
	return x*(1.5f - half_x0*x*x);
}

where INV_SQRT_NEWTON_N is a magic number is chosen to minimize the error. Depending on which error one would like to minimize, be it the 1-, 2-, or ∞-norm, different magic numbers need to be used as is shown in Table 2.

Table 2. Optimal magic numbers for the three norms with one step of Newton's method.

Magic Number
INV_SQRT_NEWTON_N		1-Norm of
Relative Error		2-Norm of
Relative Error		∞-Norm of
Relative Error
15972923570.00065200.0010780.002988
15973763220.00072460.00094830.002338
15974631750.00095490.0011180.001751

The last number is one smaller that the number recommended by David Eberly in his 2002 paper.

Figures 4 through 6 show the relative error of the approximations of 1/√x for values of x between 0.5 and 8 for this modification. As with the standard function, the relative error repeats for each power of 4. Figures 4, 5, and 6 plot the error when using the constant which minimizes the 1-, 2-, and ∞-norms, respectively.


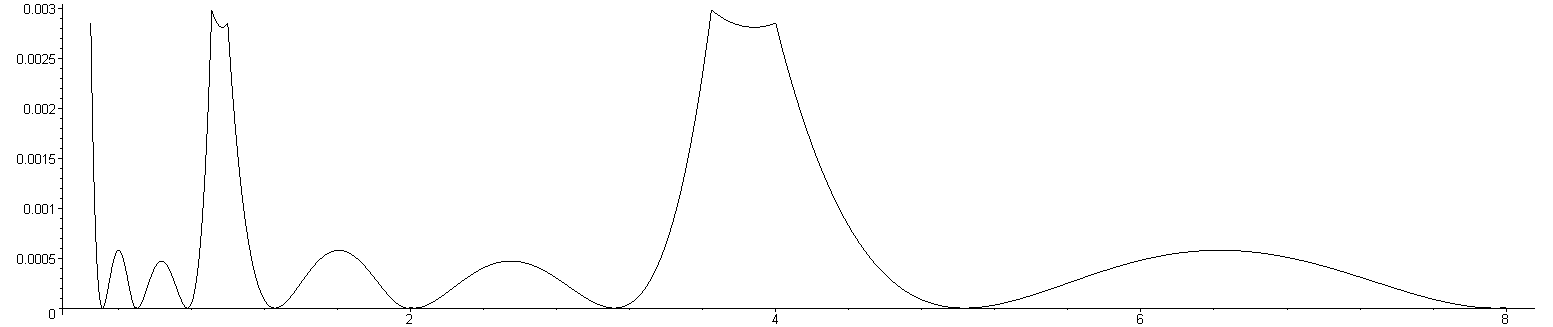
Figure 4. The relative error for the coefficient minimizing the 1-norm of the relative error with Newton's method.


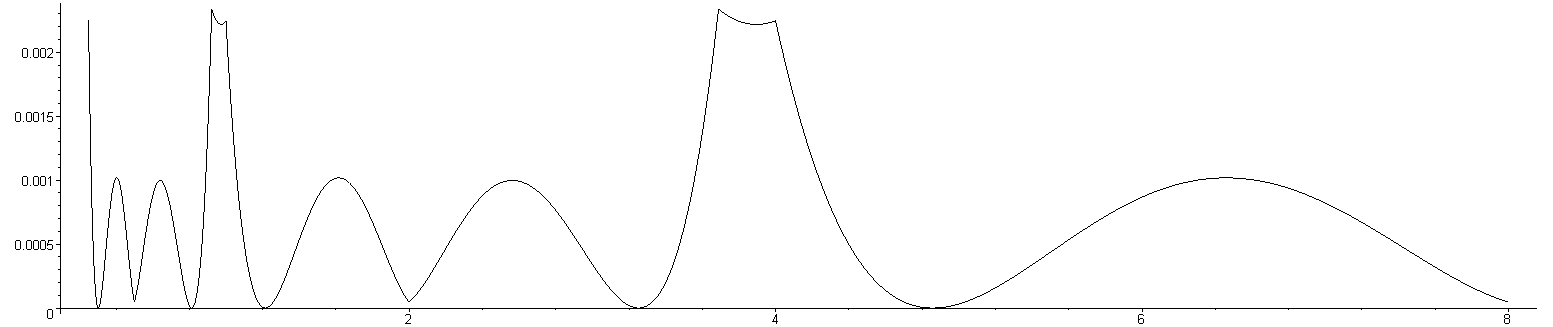
Figure 5. The relative error for the coefficient minimizing the 2-norm of the relative error with Newton's method.


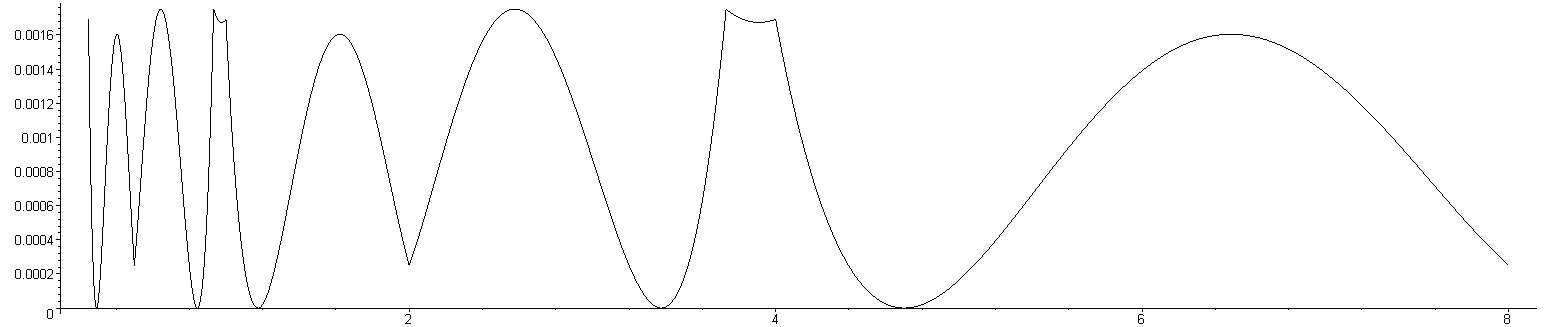
Figure 6. The relative error for the coefficient minimizing the ∞-norm of the relative error with Newton's method.

At the cost of five floating-point operations (four multiplications and one subtraction), the error is reduced by a factor of 20.

A Proposed Further Optimization

Looking at Figures 4-6, one may note that the relative error is nonnegative after one application of Newton's method. This is a natural consequence of Newton's method and is not because the image is drawing the absolute value of the error. Do demonstrate this visually, consider Figure 7 which shows 1/x2 − 2, the root of which is 1/√2.


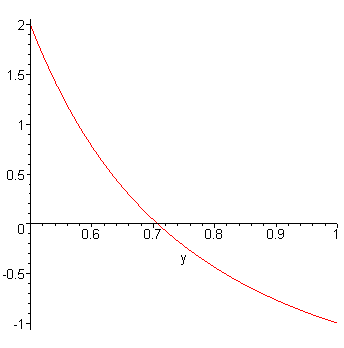
Figure 7. The function 1/x2 − 2 with root 1/√2 &asympt; 0.7071.

An underestimate which is sufficiently close to the actual value will continue to underestimate the root, as is shown in Figure 8 which starts with the approximation 0.6 and, after one iteration of Newton's method, is 0.684.


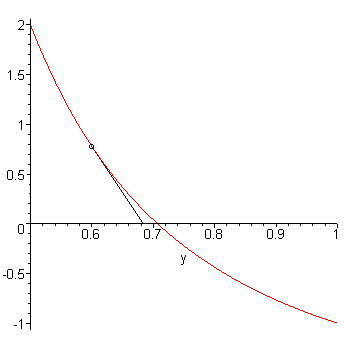
Figure 8. The approximation 0.6 to the value 1/√2 and one iteration of Newton's method.

An overestimate which is sufficiently close to the actual value,however, will underestimate the root with the next approximation, as is shown in Figure 9 which starts with the approximation 0.8 and, after one iteration of Newton's method, is 0.688···.


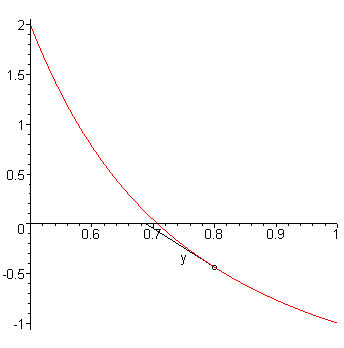
Figure 9. The approximation 0.8 to the value 1/√2 and one iteration of Newton's method.

Consequently, one further multiplication can be used to reduce the error yet again by approximately 50% by centering the result. A significant bonus is that the multiplier occurs on the result; however, we can absorb the multiplication into two constants which are already being used—in essence, we get the multiplications for free.

float inv_sqrt_newton( float x ) {
	float const mx = 0.5f*MULTIPLIER*x;
	int xi = *reinterpret_cast<int *>( &x );
	xi = INV_SQRT_NEWTON_N - (xi >> 1);
	x = *reinterpret_cast<float *>( &xi );
	return x*(1.5f*MULTIPLIER - mx*x*x);
}

Using the appropriate multipliers to reduce the approximation, as is shown in Figures 10 through 12.


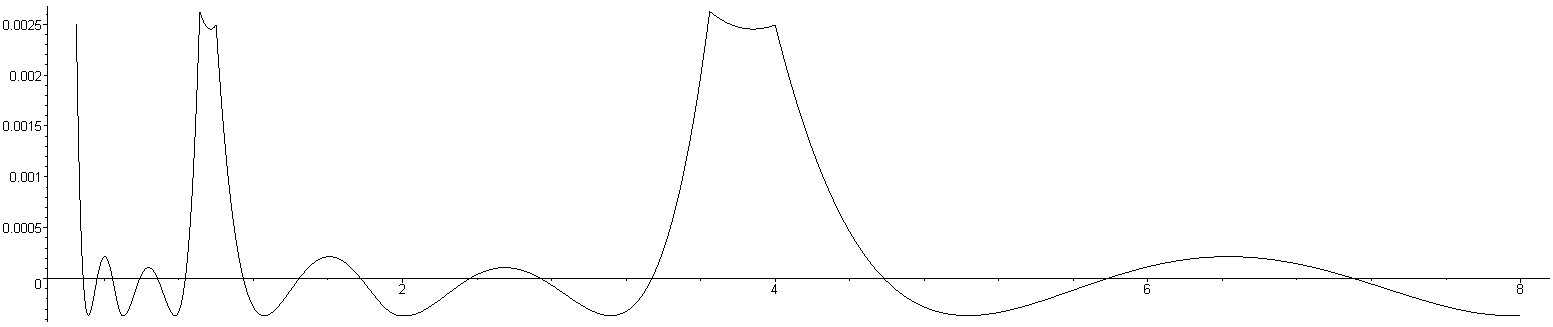
Figure 10. The relative error for the coefficient minimizing the 1-norm of the relative error with Newton's method and a multiplier.


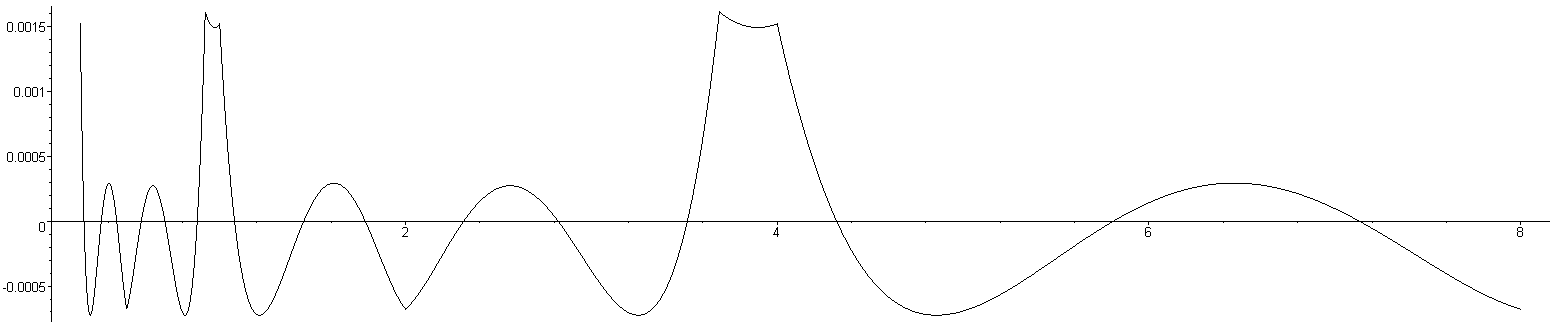
Figure 11. The relative error for the coefficient minimizing the 2-norm of the relative error with Newton's method and a multiplier.


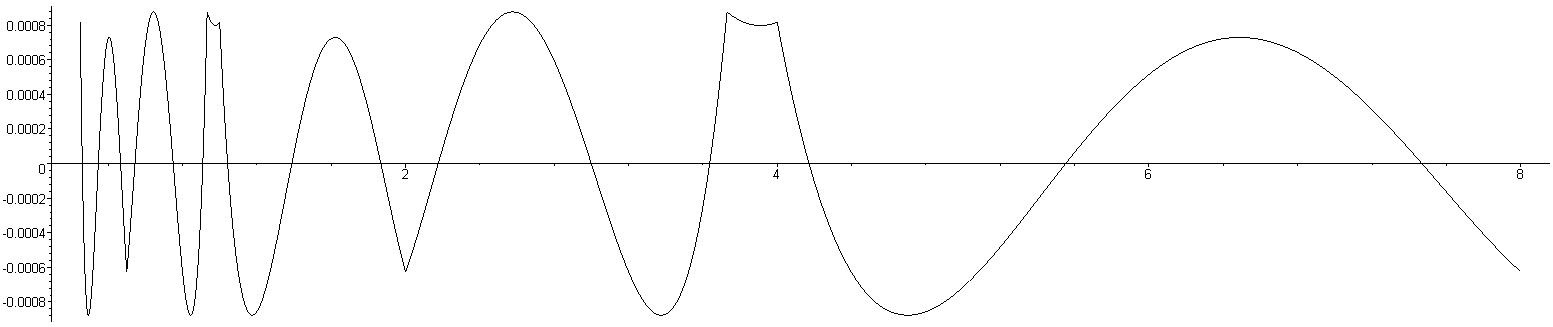
Figure 12. The relative error for the coefficient minimizing the ∞-norm of the relative error with Newton's method and a multiplier.

Table 2. Optimal magic numbers for the three norms with one step of Newton's method.

NormMULTIPLIERError
1-Norm1.0003632458114620.0005151
2-Norm1.0007247683715820.0006122
∞-Norm1.0008763113021850.0008765

What is possibly surprising is that this does not seem to increase the run time as there are already a number of floating-point multiplications into which this additional operation could be wrapped into.

Trial Runs

Approximating the integral of 1/sqrt(x) using a Riemann sum from 0 to 2^22, we get the following run times:

  • Using sqrt and floating-point division: 3.396s.
  • Using inv_sqrt_multiplier: 1.147
  • Using inv_sqrt_newton: 1.118
  • Using inv_sqrt: 0.837

While papers claim that time is reduced to 25% of that using no calculations, I only get a reduction to 33%; however, I will assume that is a result of my ignorance. What is fascinating; however, is that the addition of the multiplier only degrades the performance of Newton's method by less than 3%.

The Magic Number of 1597463007/0x5f3759df

The recommended magic number 1597463007 does not appear to minimize any of the norms listed above. The wikipedia page and the references therefrom do not shed further light as to why this specific value was chosen. It would be interesting to know why that value was chosen over a value which minimizes the relative error subject to a specific norm. Chris Lomont suggests another constant which is only one unit away from the optimal constant minimizing the ∞-norm.

Function Plots

Figures 13 and 14 plot 1/√x versus inv_sqrt(x) and inv_sqrt_multiplier(x), respectively. The first image shows clearly that the approximation is not very good; however, the second is almost visually indistinguishable.


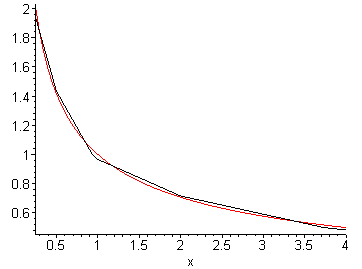
Figure 13. A plot of 1/√x and inv_sqrt(x) on [0.25, 4].


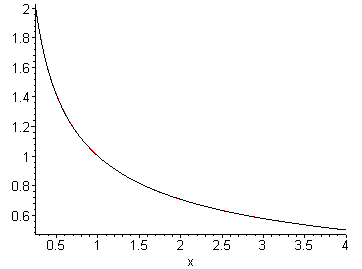
Figure 14. A plot of 1/√x and inv_sqrt_multiplier(x) on [0.25, 4].

References

Thanks to Ryan Fox for suggesting this topic.